ELEKTROMAGNETIZMAS
9 SKYRIUS. ELEKTROS LAUKAS VAKUUME
Lauko stiprumas
Eksperimentiškai buvo nustatyta, kad dalelės gali patirti daug stipresnę sąveiką nei gravitacinės. Norėdami tai paaiškinti masėms m dalelės pridėjo dar vieną dalelių charakteristiką - elektros krūvis q, matuojamas pakabučiai(Cl).
Vadinkime įkrautą dalelę, t.y. dalelę, kuri turi krūvį q, taškinis mokestis q(priešingai nei įkrautas kūnas, kurio matmenys negali būti ignoruojami šios problemos sąlygomis). Kiekvienas stacionarus krūvis yra taškinis q kuria supančioje erdvėje elektrinis laukas(tiksliau elektrostatinis laukas). Bet koks kitas taškinis mokestis šiame lauke turės įtakos elektrinė jėga :
kur vadinamas vektorius įtampa elektrinis laukas toje vietoje, kur yra užtaisas. Jėga gali būti nukreipta į krūvį arba į jį q arba nuo jo. Šiuo atžvilgiu buvo įvesti du krūvio tipai: teigiamas ir neigiamas. Priešingi krūviai traukia, o panašūs krūviai vienas kitą atstumia (31.1 pav.).
Įtempimas apibrėžiamas kaip jėga, veikianti vienetinį teigiamą taškinį krūvį tam tikrame lauko taške:
kur > 0. Iš (31.2) išraiškos aišku, kad matmuo yra niutonas kulonui (N/C).
Patirtis rodo, kad judantis taškas įkrauna q kuria per atstumą rįtampa nuo jo
(31.3)
čia ε 0 yra elektrinė konstanta (ε 0 = 8,85 10 –12 C 2 /(N m 2)), yra spindulio vektoriaus vienetinis vektorius, nubrėžtas iš lauko centro, esantis koordinačių pradžioje, yra taškinis krūvis q, į mus dominančią sritį.
Iš išraiškos (31.1) aišku, kad elektros jėga, veikianti krūvį, yra nukreipta ta pačia kryptimi kaip ir vektorius, jei krūvis yra teigiamas, ir priešingas vektoriui, jei krūvis neigiamas (31.2 pav.).
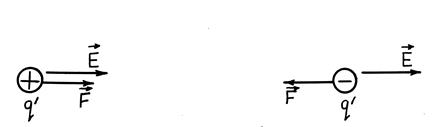
Iš patirties matyti, kad sistemos lauko stiprumas N stacionarūs taškiniai krūviai
kur yra lauko stiprumas mus dominančiame taške, sukurtas i-taškinis mokestis, jei nėra kitų taškinių mokesčių. Santykis (31.4) išreiškia elektrinių laukų superpozicijos principas.
31.1 pavyzdys. Du 0,3 kg masės rutuliai yra išdėstyti tokiu atstumu, kad jų krūvių sąveiką subalansuotų gravitacinės traukos jėga. Raskite rutuliukų spindulius, jei rutuliukų paviršiaus krūvio tankis 
| Duota: m 1 = m 2 = m=0,3 kg F e = F gr R 1 = R 2 = R | Sprendimas 
.
F e = F gr. 
|
||||
| R – ? |
Atsakymas:R= 4 cm.
31.2 pavyzdys. Taškiniai mokesčiai q 1 = 2q Ir q 2 = – q yra taip, kaip parodyta pav. 31.4. Atstumas tarp įkrovų yra d. Nustatykite, kokiu atstumu x 1 nuo mokesčio q 1 elektrinio lauko stipris lygus nuliui.
| Duota: q 1 = 2q q 2 = – q d E( x 1) = 0 | Sprendimas  Ryžiai. 31.3 |
| x 1 – ? |
Pagal elektrinių laukų superpozicijos principą taške, kuriame turi būti įvykdyta sąlyga
kur ir yra krūvių sukuriami lauko stiprumai q 1 ir q 2 šiuo metu. Akivaizdu, kad ši sąlyga nebus įvykdyta už ašies ribų x(vektoriai ir yra nukreipti vienas kito kampu), taip pat į ašį xį kairę nuo krūvio q 1 kur visada E 1 > E 2 (žr. (31.3) formulę ir uždavinio sąlygą). Tarp ašies krūvių x negali būti lygus nuliui, nes vektoriai ir yra nukreipti ta pačia kryptimi. Belieka manyti, kad norimas taškas yra ant ašies x kaltinimo dešinėje q 2 (žr. 31.3 pav.). Atstumas x 1 nuo mokesčio q 1 randame iš sąlygos
Sumažinkime ir paimkime kvadratinę šaknį iš kairės ir dešinės lygybės pusių:
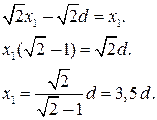
Atsakymas: x 1 = 3,5 d.
§ 32. Vektoriaus srautas
Vektorinis laukas vizualiai pavaizduotas naudojant vektorines linijas kurios atliekamos taip:
1) jų liestinė kiekviename taške sutampa su vektoriaus kryptimi;
2) tiesių, prasiskverbiančių į vienetinį paviršiaus plotą, statmeną tiesėms, skaičius (linijos tankis) lygus vektoriaus moduliui (32.1 pav.).
Elektrinis laukas vadinamas vienalytis, jei kiekviename lauko taške vektorius = const. Tokio lauko vektorinės linijos lygiagrečios ir atstumai tarp jų vienodi (32.2 pav.).
Ryžiai. 32.1 pav. 32.2
Vektorinės linijos elektrostatinis laukas prasideda teigiamais krūviais ir baigiasi neigiamais krūviais.
Paimkime elementarią svetainę dS vektoriniame lauke (32.3 pav.). Leisti yra vienetas normalus vektorius svetainėje dS, α yra kampas tarp vektorių ir . Tada vektorinių linijų auskarų skaičius dS, lygus
kur yra vektorius, kurio modulis lygus dS, o kryptis sutampa su vieneto normaliojo vektoriumi į vietą dS.
Paskambinkime F vektoriaus srautas per savavališką paviršių S vektorinių linijų, prasiskverbiančių į šį paviršių, skaičius. Akivaizdu,
paviršiaus integralas S iš vektorių skaliarinės sandaugos ir . Srautas yra algebrinis dydis. Srauto ženklas priklauso nuo įprastos krypties pasirinkimo dS. Uždariems paviršiams įprasta paimti išorinį normalų.
§ 33. Gauso teorema vektoriniam laukui
Teorema. Vektoriaus srautas per bet kurį uždarą paviršių S lygus q ext. /ε 0 , kur q ext. - algebrinė krūvių suma šio paviršiaus viduje:
(33.1)
kur apskritimas šalia integralo reiškia, kad integravimas atliekamas per uždarą paviršių.
Teoremos įrodymas. Panagrinėkime vienos stacionarios elektrinį lauką taškinis mokestis q. Leisti q> 0. Protiškai apgaukime krūvį q savavališkai uždaras paviršius S(33.1 pav.).
Raskime srautą d F vektorius per elementą dS paviršiai. Akivaizdu,
Kur 
- elementarus vientisas (erdvinis) kampas kūgio viduje, ant kurio remiasi dS, kurio viršūnė yra įkrovimo vietoje q.
Vektoriaus srautas per visą uždarą paviršių S
kur yra bendras erdvės kampas. Mes turime
kuri sutampa su išraiška (33.1).
Dabar apsvarstykite sistemos sukurtą elektrinį lauką N stacionarių taškinių krūvių Protiškai apjuoskime šią krūvių sistemą savavališku uždaru paviršiumi S. Naudodamiesi elektrinių laukų superpozicijos principu, galime rašyti
Kur q- algebrinė suma N krūviai, kurie sutampa su išraiška (33.1).
Gauso teorema kai kuriais atvejais leidžia labai paprastai nustatyti stiprumą bet kuriame elektrinio lauko taške.
33.1 pavyzdys. Turime begalinę vienodai įkrautą plokštumą paviršiaus tankisįkrauti σ. Nustatykite įtampą O yra E x iš lėktuvo.
Per mus dominantį tašką nubrėžkime uždarą Gauso paviršių S cilindro pavidalu simetriškai plokštumos atžvilgiu taip, kad taškas būtų cilindro apačioje (32.2 pav.). Raskime vektoriaus srautą per Gauso paviršių:
Kur S pagrindinis - cilindro pagrindo plotas. Integruodami atsižvelgėme į tai, kad vektoriaus srautas per šoninį cilindro paviršių yra lygus nuliui (vektoriaus linijos neprasiskverbia į šį paviršių) ir visuose cilindro pagrindo taškuose α = 0 ir E= konst.
Pagal Gauso teoremą
kur yra plokštuminis krūvis, sutelktas cilindro viduje. Suraskime jį. Pagal apibrėžimą paviršiaus krūvio tankis
Esant vienodai įkrautai plokštumai (σ = const) galime rašyti
(iš 33.2 pav. aišku, kad krūvis sutelktas plokštumos dalyje su plotu S pagrindinis), iš kur
(33.4)
Pakeitę išraiškas (33.2) ir (33.4) į santykį (33.3), gauname
Iš (33.5) išraiškos aišku, kad E nepriklauso nuo atstumo x iš įkrauto lėktuvo, t.y.
Todėl begalinės tolygiai įkrautos plokštumos sukurtas elektrinis laukas yra vienodas.
33.2 pavyzdys. Turime vienodai įkrautą sferą, kurios paviršiaus krūvio tankis σ. Sferos spindulys R. Nustatykite įtampą O yra E elektrinis laukas per atstumą r nuo sferos centro.
(iš 33.3 pav. aišku, kad Gauso paviršiaus viduje nėra krūvio), vadinasi,
Vadinasi, įkrautos sferos viduje atsiranda įtampa E elektrinis laukas lygus nuliui.
Dabar apibrėžkime E taške, esančiame už įkrautos sferos ribų ( r> R). Tegul sfera yra teigiamai įkrauta. Dėl simetrijos vektorius E Sferos sukurtas laukas mus dominančiame taške yra nukreiptas radialiai iš sferos centro.
E= konst.
Pagal Gauso teoremą
Iš pav. 33.3 aišku, kad įkrauta sfera yra Gauso paviršiaus viduje, taigi ir krūvis q ext. lygus įkrovimui q sf. sferos. Tolygiai įkrautos sferos atveju (σ = const) galime rašyti
(33.8)
Pakeitę išraiškas (33.6) ir (33.8) į santykį (33.7), gauname
Todėl įtampa E laukas už įkrautos sferos mažėja didėjant atstumui r. Grafinė priklausomybė E(r) tolygiai įkrautos sferos elektrinio lauko parodyta fig. 33.4.
33.3 pavyzdys. Turime vienodai įkrautą rutulį, kurio tūrinis krūvio tankis ρ. Rutulio spindulys R. Nustatykite įtampą O yra E elektrinis laukas per atstumą r nuo kamuolio centro.
Integruodami atsižvelgėme į tai, kad visuose Gauso sferos taškuose α = 0 ir E= konst.
Pagal Gauso teoremą
kur yra rutulio dalies krūvis, sutelktas Gauso sferoje. Suraskime jį. Pagal apibrėžimą tūrio krūvio tankis
Esant vienodai įkrautam rutuliui (ρ = const) galime rašyti
kur yra rutulio tūris Gauso sferoje. Iš (33.12) išraiškos randame
(33.13)
Pakeitę išraiškas (33.10) ir (33.13) į santykį (33.11), gauname
Jei į elektros krūvį supančią erdvę įvedamas kitas krūvis, tada jį veiks Kulono jėga; Tai reiškia, kad erdvėje, supančioje elektros krūvius, yra jėgos laukas. Remiantis šiuolaikinės fizikos sampratomis, laukas tikrai egzistuoja ir kartu su materija yra viena iš materijos egzistavimo formų, per kurią vyksta tam tikra sąveika tarp makroskopinių kūnų ar dalelių, sudarančių medžiagą. Šiuo atveju kalbame apie elektrinį lauką – lauką, per kurį sąveikauja elektros krūviai. Mes laikome elektrinius laukus, kuriuos sukuria stacionarūs elektros krūviai ir vadinami elektrostatinės.
Jis naudojamas elektrostatiniam laukui aptikti ir eksperimentuoti bandomoji vieta teigiamas krūvis - toks krūvis, kuris neiškreipia tiriamo lauko (nesukelia lauką sukuriančių krūvių perskirstymo). Jei įkrovos sukurtame lauke Q, atlikti bandomąjį mokestį K 0, tada jį veikia jėga F, skiriasi skirtinguose lauko taškuose, o tai pagal Kulono dėsnį yra proporcinga bandomajam krūviui K 0 . Todėl santykis F/ K 0 nepriklauso nuo K 0 ir apibūdina elektrostatinį lauką taške, kuriame yra bandomasis krūvis. Šis dydis vadinamas įtampa ir yra elektrostatiniam laukui būdinga jėga.
Elektrostatinio lauko stiprumasšiuo metu yra fizinis kiekis, nustatoma pagal jėgą, veikiančią bandymo vieneto teigiamą krūvį, esantį šiame lauko taške:
Taškinio krūvio lauko stiprumas vakuume
Vektoriaus E kryptis sutampa su teigiamą krūvį veikiančios jėgos kryptimi. Jei lauką sukuria teigiamas krūvis, vektorius E nukreipiamas išilgai spindulio vektoriaus iš krūvio į išorinę erdvę (testo teigiamo krūvio atstūmimas); jei laukas sukurtas neigiamas krūvis, tada vektorius E nukreiptas į krūvį (pav.).
Elektrostatinio lauko stiprio vienetas yra niutonas kulonui (N/C): 1 N/C – lauko, veikiančio 1 C taškinį krūvį 1 N jėga, intensyvumas; 1 N/C = 1 V/m, kur V (voltas) yra elektrostatinio lauko potencialo vienetas. Grafiškai elektrostatinis laukas pavaizduotas naudojant įtempimo linijos - tiesių, kurių liestinės kiekviename taške sutampa su vektoriaus E kryptimi (pav.).
Kadangi bet kuriame erdvės taške įtempimo vektorius turi tik vieną kryptį, įtempimo linijos niekada nesikerta. Dėl vienodas laukas(kai įtempimo vektorius bet kuriame taške yra pastovus pagal dydį ir kryptį) įtempimo linijos yra lygiagrečios įtempimo vektoriui. Jei lauką sukuria taškinis krūvis, intensyvumo linijos yra radialinės tiesios linijos, kylančios iš krūvio, jei jis yra teigiamas (1 pav.). A) ir įtraukiamas į jį, jei krūvis yra neigiamas (1 pav.). b). Dėl didelio aiškumo elektrostatinio lauko grafinis vaizdavimo metodas plačiai naudojamas elektrotechnikoje.
Tam, kad įtempimo linijas būtų galima apibūdinti ne tik elektrostatinio lauko krypčiai, bet ir jo intensyvumo vertei, buvo sutarta jas nubrėžti tam tikru tankiu: įtempimo linijų, prasiskverbiančių į įtempimui statmeną paviršiaus ploto vienetą, skaičių. linijos turi būti lygios vektoriaus E moduliui. Tada įtempimo linijų, prasiskverbiančių į elementariąją sritį d, skaičius S, normalus n kuri sudaro kampą a su vektoriumi E, lygus E d Scos a = E n d S, Kur E p- vektorinė projekcija Eį normalią nį svetainę d S(ryžiai.).
Reikšmė dФ E =E n dS= E dS vadinamas įtampos vektoriaus srautas per platformą d S.Čia d S=d Sn- vektorius, kurio modulis yra d S, o kryptis sutampa su normaliosios krypties nį svetainę. Vektoriaus krypties pasirinkimas n(ir todėl d S) yra sąlyginis, nes gali būti nukreiptas bet kuria kryptimi. Elektrostatinio lauko stiprumo vektoriaus srauto vienetas yra 1 V×m.
Savavališkam uždaram paviršiui S vektoriaus srautas E per šį paviršių
,
kur integralas perimtas per uždarą paviršių S. Srauto vektorius E yra algebrinis dydis: priklauso ne tik nuo lauko konfigūracijos E, bet ir dėl krypties pasirinkimo n. Uždarytiems paviršiams laikoma teigiama normaliosios krypties kryptis išorinis normalus, tai yra normalus, nukreiptas į išorę į paviršiaus padengtą sritį.
Kulono jėgoms taikomas jėgos veikimo nepriklausomumo principas, t.y., iš lauko veikianti jėga F bandomąjį krūvį Q 0 yra lygi jėgų Fi vektorinei sumai, kurią jį veikia kiekvienas iš krūvių Q i: . F = Q 0 E ir F i = Q 0 E i , kur E – susidariusio lauko stiprumas, o E i – krūvio Q i sukurto lauko stiprumas. Pakeitę tai aukščiau esančia išraiška, gauname . Ši formulė išreiškia elektrostatinių laukų superpozicijos (uždėjimo) principą, pagal kurį krūvių sistemos sukurto lauko stipris E yra lygus kiekvieno krūvio tam tikrame taške sukuriamų lauko stiprių geometrinei sumai. atskirai.
Elektrinio dipolio elektrostatiniam laukui apskaičiuoti taikomas superpozicijos principas. Elektrinis dipolis – tai dviejų vienodo dydžio (+Q, –Q) priešingų taškinių krūvių sistema, tarp kurių atstumas l yra žymiai mažesnis už atstumą iki nagrinėjamų lauko taškų. Pagal superpozicijos principą dipolio lauko stipris E savavališkame taške 
, kur E+ ir E– yra atitinkamai teigiamų ir neigiamų krūvių sukuriami lauko stiprumai.
Kiekvienas elektros krūvis yra apsuptas elektrinio lauko. Ilgalaikių tyrimų metu fizikai priėjo prie išvados, kad įkrautų kūnų sąveika vyksta dėl juos supančių elektrinių laukų. Jie yra ypatinga materijos forma, neatsiejamai susijusi su kiekviena elektros krūvis.
Elektrinio lauko tyrimas atliekamas įvedant į jį mažus įkrautus kūnus. Šie kūnai vadinami „bandomaisiais mokesčiais“. Pavyzdžiui, įkrautas kamštienos rutulys dažnai naudojamas kaip bandomasis įkrovimas.
Įvedant bandomąjį krūvį į teigiamą krūvį turinčio kūno elektrinį lauką, jo veikiamas šviesiai teigiamai įkrautas kamštienos rutulys kuo labiau nukryps, kuo arčiau jį priartinsime prie kūno.
Judindami bandomąjį krūvį savavališkai įkrauto kūno elektriniame lauke, nesunkiai pastebėsite, kad skirtingose vietose jį veikianti jėga skirsis.
Taigi, viename lauko taške paeiliui dedant skirtingų dydžių q1, q2, q3, ..., qn bandomuosius teigiamus krūvius, galima pastebėti, kad juos veikiančios jėgos F1, F2, F3, ..., Fn , yra skirtingi, tačiau jėgos ir tam tikro krūvio dydžio santykis tokiame lauko taške nesikeičia:
F1/q1 = F2/q2 = F3/q3 = … = Fn/qn.
Jei taip išnagrinėsime skirtingus lauko taškus, gautume tokią išvadą: kiekvienam atskiram elektrinio lauko taškui jėgos, veikiančios bandomąjį krūvį, ir tokio krūvio dydžio santykis nekinta. ir nepriklausomai nuo bandomojo krūvio dydžio.
Iš to išplaukia, kad šio santykio dydis apibūdina elektrinį lauką savavališkame taške. Dydis, matuojamas jėgos, veikiančios teigiamą krūvį, esantį šiame lauko taške, ir krūvio dydžio santykiu, yra elektrinio lauko stiprumas:
Jis, kaip matyti iš jo apibrėžimo, yra lygus jėgai, kuri veikia teigiamo krūvio vienetą, esantį tam tikrame lauko taške.
Elektrinio lauko stiprio vienetas imamas veikti vieno elektrostatinio vieneto dydžio krūvį vieno dyno jėga. Šis vienetas vadinamas absoliučios elektrostatinės įtampos vienetu.
Norint nustatyti bet kurio taškinio krūvio q elektrinio lauko stiprumą savavališkame tam tikro krūvio lauko A taške, esančiame atstumu r1 nuo jo, šiame savavališkame taške reikia įdėti bandomąjį krūvį q1 ir apskaičiuoti jėgą Fa. kad jį veikia (vakuumui).
Fa = (q1q)/r²₁.
Jei imsime jėgos, turinčios įtakos krūviui, dydžio santykį su jo verte q1, tada galime apskaičiuoti elektrinio lauko stiprumą taške A:
Be to, įtampą galite rasti savavališkame taške B; jis bus lygus:
Todėl taškinio krūvio elektrinio lauko stipris tam tikrame lauko taške (vakuume) bus tiesiogiai proporcingas duoto krūvio dydžiui ir atvirkščiai proporcingas atstumo tarp šio krūvio ir taško kvadratui.
Lauko stiprumas veikia kaip jo galios charakteristika. Žinant jį savavališkame lauko E taške, nesunku apskaičiuoti jėgą F, veikiančią krūvį q tam tikrame taške:
Laukai – įtempimo kryptis kiekviename konkrečiame lauko taške bus suderinta su jėgos, veikiančios taške esantį teigiamą krūvį, kryptimi.
Kai lauką sudaro keli krūviai: q1 ir q2, intensyvumas E bet kuriame šio lauko taške A bus lygus intensyvumo E1 ir E2, kurį tam tikrame taške sukuria atskirai krūviai q1 ir q2, geometrinei sumai.
Elektrinio lauko stiprumas savavališkame taške gali būti rodomas grafiškai, naudojant nukreiptą segmentą, kuris kyla iš šio taško, panašiai kaip jėgos ir kitų vektorinių dydžių vaizdavimas.
